はじめに
このブログをもっと頻繁に更新していきたいと思っていたので、手始めに月刊ブログと題して月の終わりに近況報告と制作物のまとめの記事を書いていこうと思います。今回が第一回です。
近況報告
大学を退学しました
龍谷大学という大学に通っていましたが、持病の都合などで退学することになりました。休学期間が長く授業にはほとんど出席していませんでしたが、幾何学の研究室に居候させてもらったり3Dプリンターなどが置かれているファブリケーション施設で遊んだりと、模範的とは言えないながらも楽しい大学生活を送りました。ちなみに大学入学前に通っていた高専も3年次で退学しているので、最終学歴は中卒です。
今後の進路は未定で、今は兎にも角にも外で人並みに活動できる体力をつけなければという段階です。
3Dデータの販売を始めました
大学を退学することになり所謂ニートのような生活になるので、なんとか収入を得なければと思い2か月ほど前から3Dプリント用のSTLファイルをCult.というプラットフォームで販売し始めました。これが思っていたより好評で、300~400円のデータが合計で50個以上売れて、3Dプリンターの維持費を賄える程度の収入を得ることができています。本当にありがとうございます。
ご興味があればこれを読んでいる3Dプリンター所持者の方もデータを購入して遊んでみてもらえると嬉しいです。無料のデータもいくつか公開しています。
https://cults3d.com/en/users/KeishiroUeki/
デザインフェスタvol.58に出展します
2023年11月11-12日に東京で開催されるデザインフェスタに両日参加します。分野の近いX (Twitter)のフォロワーが出展しているのを見てノリと勢いで参加申し込みをしましたが、一度も現地に行ったことがないので雰囲気が全く分からないしこういった展示のノウハウもほとんど無いしで今になって不安になってきています。体力面でも心配が尽きません。が、なんとかぼちぼち頑張ります。
デザインフェスタvol.58開催概要
9月の創作物まとめ
Trammel of Archimedes

Trammel of Archimedesと呼ばれる機構を3Dプリントしました。スライダなどが組みあがった状態で3Dプリントされるprint in placeなモデルとして設計しました。
Dudeny dissection

Henry Dudeneyが考案したパズルで、切り分けられた正方形と正三角形が入れ替わります。フレームを白いTPU(柔らかい素材)で3Dプリントし、そこに4色の図形をはめ込むことで折り曲げを可能にしています。投稿後に気が付きましたが、作図時に寸法を間違えていたようで正方形が歪んでしまっていました。
Hinged tessellation

交互に配置された赤と青の図形が回転し、敷き詰め模様を形成します。先ほど紹介したDudeny dissectionと同様にTPUのフレームを使って構成されています。
参考
apu. https://x.com/apu_yokai/status/1490272050564730881?s=20
荒木義明 .『M.C.エッシャーと楽しむ算数・数学パズル』
正多角形を起点とする1自由度平面機構の拡張
概要
中央の正多角形から可動な平行四辺形を再帰的に配置して平行四辺形間の隙間の図形を剛体として機構を形成します。詳しい説明は後々プロジェクトの記事でするかもしれません。
正三角形
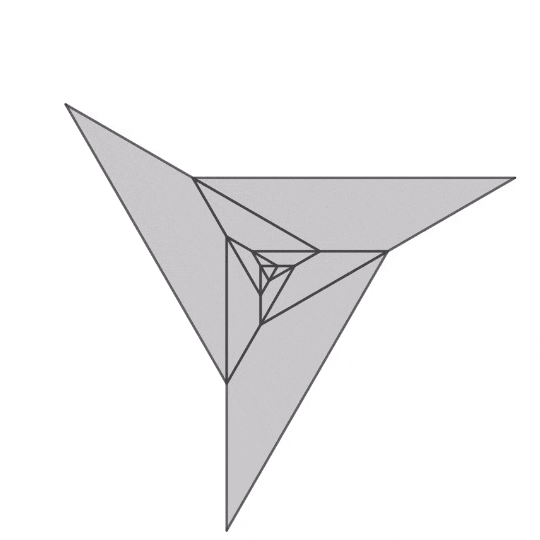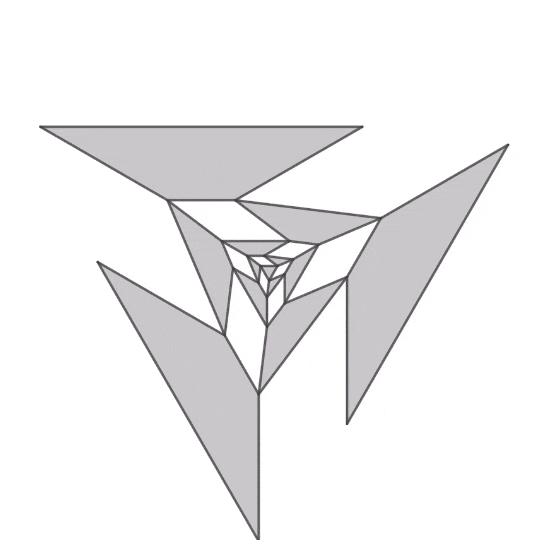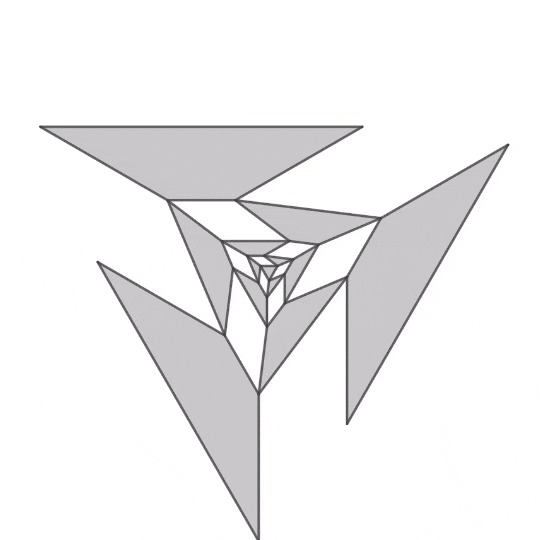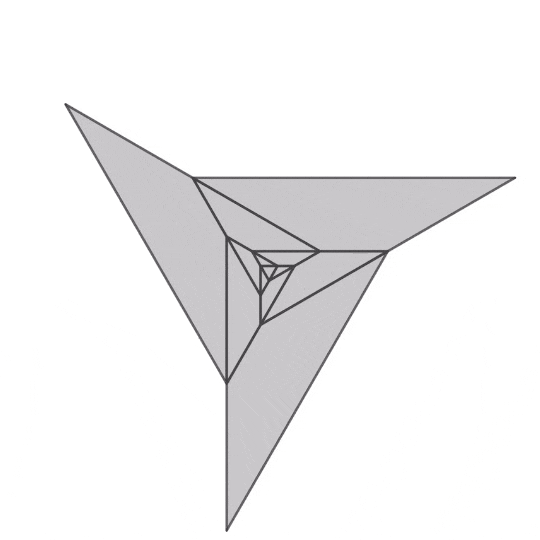
正三角形を起点とする機構のアニメーションです。
正五角形


正五角形を起点とする機構のアニメーションと実際に3Dプリントした模型です。
正六角形(変形)

正六角形を起点とする機構の各辺を相似な曲線で置換したものです。
立方体をリンクとする1自由度立体リンク機構

立方体をリンクとする1自由度立体リンク機構です。Eric AbergのGHOSTKUBEを参考にしています。
参考
Eric Aberg. https://www.youtube.com/watch?v=JaGOefhfipA
Kaleidocycle

TPUで印刷されたカレイドサイクルです。くるくると回して遊べます。60度のオーバーハングがあり、TPUで綺麗に印刷することは難しく表面が荒れている部分があります。
下記のサイトでSTLファイルを無料でダウンロードできます。
https://www.printables.com/model/595493-flexible-kaleidocycle
https://cults3d.com/en/3d-model/art/kaleidocycle-print-with-flexible-material
Hinged cubes

立方体をテープで固定して作った変形機構です。Gerard WestendorpとMartin SchwabのX (Twitter)上の投稿にインスパイアされて作成しました。

最初の構造に更に立方体を8つ追加したものです。
参考
Gerard Westendorp. https://x.com/GerardWesty31/status/1627062172164689923?s=20
Gerard Westendorp. “Hinged polyhedra and hinged Tessellations”. https://westy31.nl/Hingedpolyhedra/Hingedpolyhedra.html
Martin Schwab. https://x.com/MartinSchwab9/status/1627401247266422785?s=20
Prism linkage


角柱で構成された1自由度立体リンク機構です。これにPrism linkageと名付けて研究集会などでちょこちょこと発表したりしていました。そのうちプロジェクトの記事としっかりとまとめる予定です。
おわり