近況報告
Maker Faire Tokyo 2023に参加してきました
東京ビッグサイトで開催されていたMaker Faire Tokyoに行ってきました。たくさんの素敵な作品を見ることができてよい刺激をもらいました。来年は展示者として参加したいです。
デザインフェスタに向けて準備をしています
11月11日及び12日に東京ビッグサイトで行われるデザインフェスタvol.58に参加します。ブース番号はK-178で西館4階です。柔らかい素材(TPU)で3Dプリントした幾何学構造を展示・販売します。TPUでの3Dプリント構造に興味がある方は柔らかい素材で折り畳み構造を3Dプリントするも参照してください。
こういったリアルの催しでものを売ることは初めてなので、どれくらい在庫を用意するのか、値段はどうするかなど、わからないことが多く手探りの状態です。お手柔らかによろしくお願いします。
10月の創作物まとめ
Hinged cubes

9月に3Dプリントして作成した機構をRhinoceros+Grasshopperでアニメーションにしました。9月に作成した実物は下のGIFになります。

TPU折り紙

先月大学を退学したのですが、そこでの元後輩とLINEでやりとりをしていると、彼女のアイコンがGeoGebraで作成された折り紙のGIFアニメーションに変わっていることに気が付きました。面白いアニメーションだと思ったので詳細を聞いてみると、和食屋に設置されていたランプシェードにインスピレーションを受けて作成したとのことでした。そのときちょうどTPUを薄く印刷することで折り紙構造のようなものを作れないかと思案していたところだったので、彼女からGeoGebraのggbファイルを借りて3DプリントのためにSTLファイルに変換し、自宅の3Dプリンターで作成しました。以下の画像は彼女が撮影した和食屋のランプシェードで、『陰翳 IN-EI ISSEY MIYAKE』というシリーズの商品のようです。

折りたたまれるように変形しているこの構造ですが、rigidな機構ではない(折り紙にはあまり詳しくないですが所謂”剛体折り”ではない)ようです。折りたたまれるためには折り目以外の部分でも変形が必要です。最初のGIFでは柔らかいTPUという材料で3Dプリントしましたが、TPUよりも硬いPLAで印刷したところうまく変形できずにパキッと折り目の部分で割れてしまいました。
凧型4節リンク機構の拡張
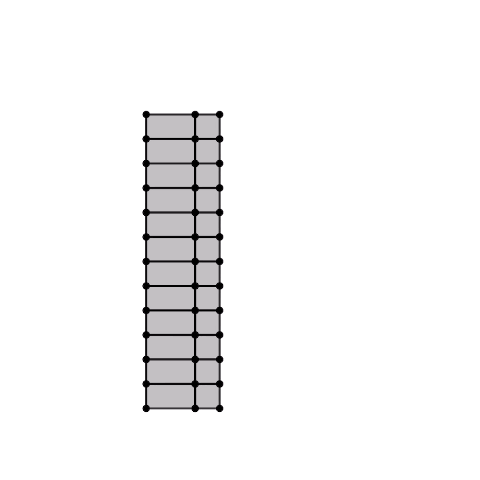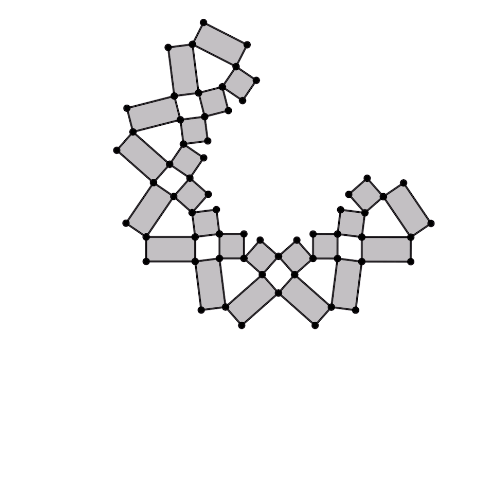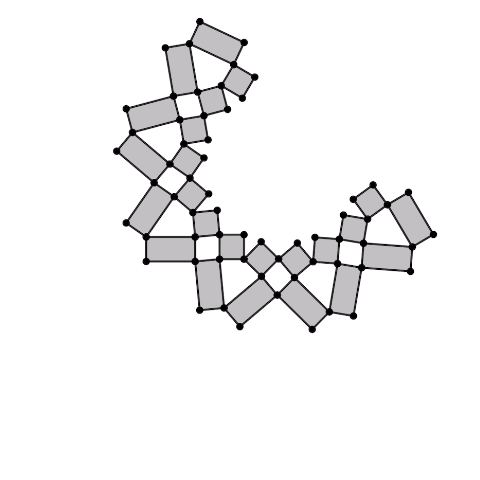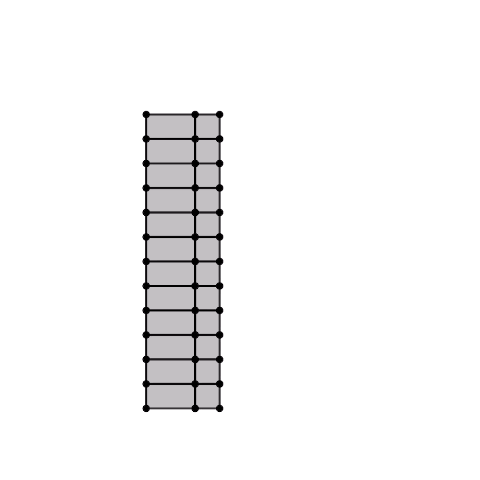
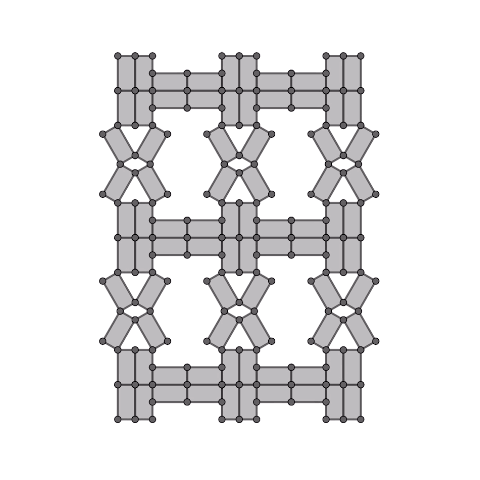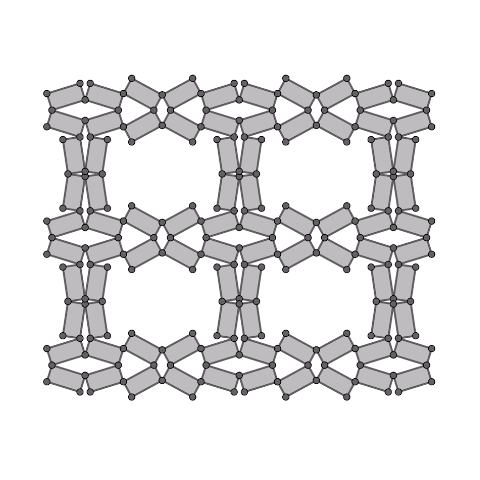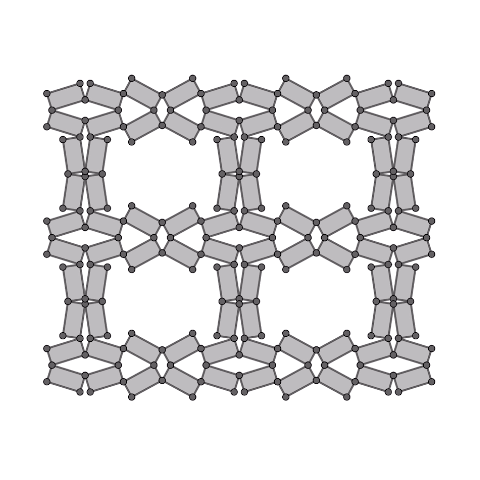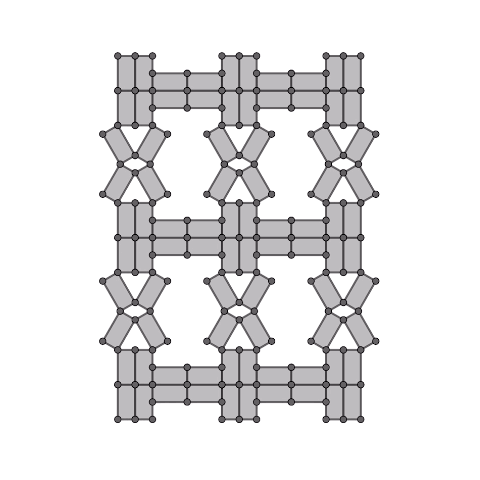
凧型の4節リンク機構の各辺から長方形(正方形)を生成し、それらを連結した1自由度機構です。
Hinged tetrahedra

複数の正四面体がヒンジで接続された1自由度機構です。このアイデアはもともと数年前のDaniel Piker(@KangarooPhysics)のツイートを基にしたものだったはずなのですが、その投稿を見つけられませんでした。
上の画像では正四面体をPLAで3Dプリントし、それらをテープで張り合わせています。


これらはTPUで全て3Dプリントしたものです。正四面体の数も増やしています。立体的な動きをする構造をTPUで印刷することは制約が多くてなかなか難しいのですが、この構造はそれぞれの正四面体の1辺が同一平面上に存在する状態が存在するので印刷が比較的簡単でした。

さらに大きくしてみました。このように波打つような動きは本来はできず、TPUの柔らかさによって許容されているものです。最初の画像にあるPLAとテープの組み合わせでこの動きをさせたらすぐに壊れてしまうでしょう。
変形に伴って光の反射が変化してキラキラしているのがお気に入りポイントです。
正三角形を基とする1自由度平面機構
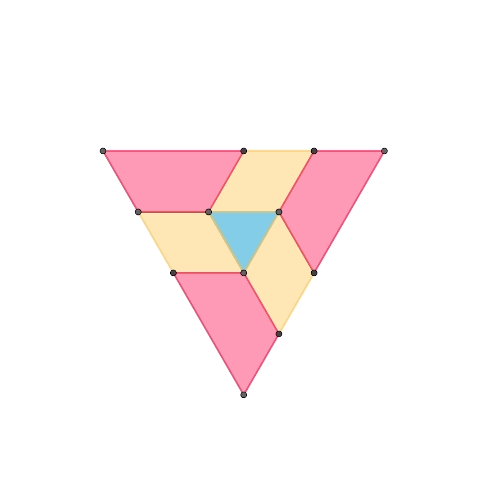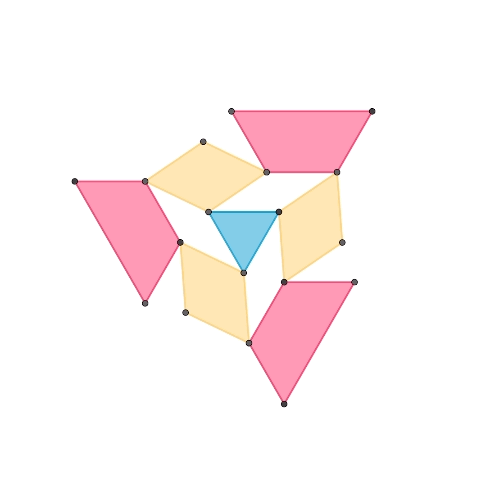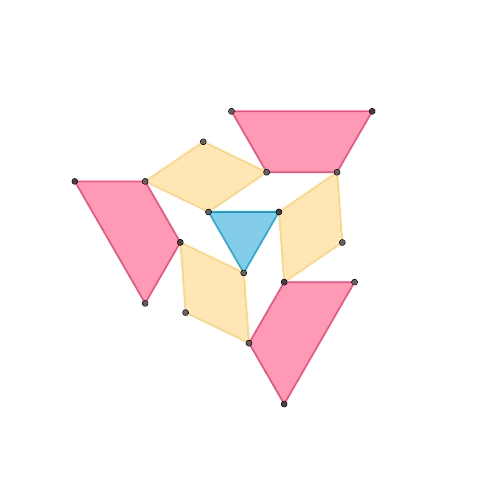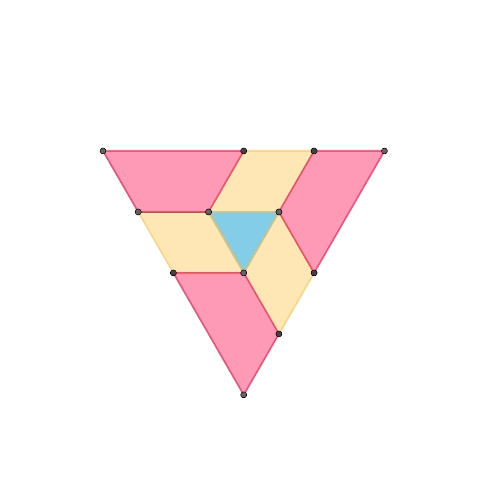
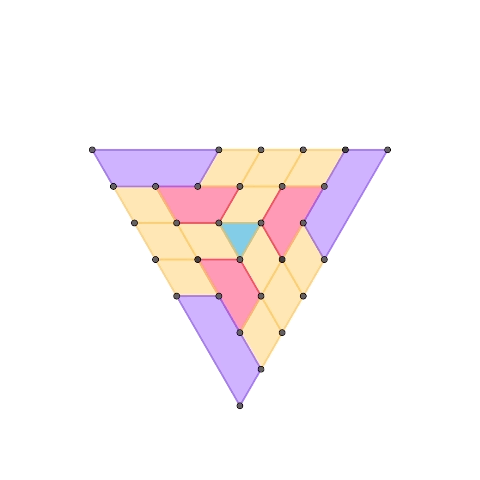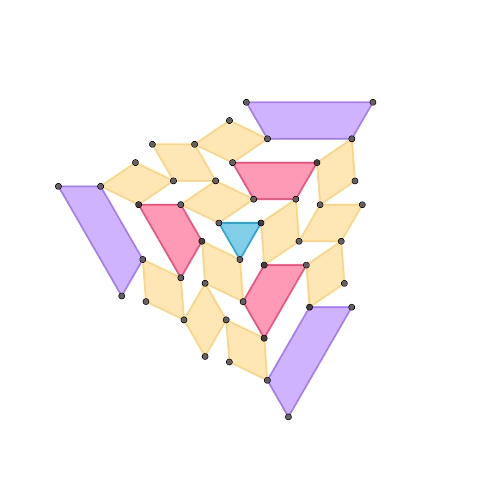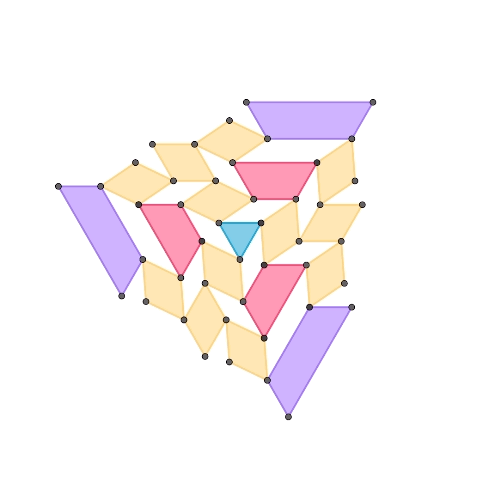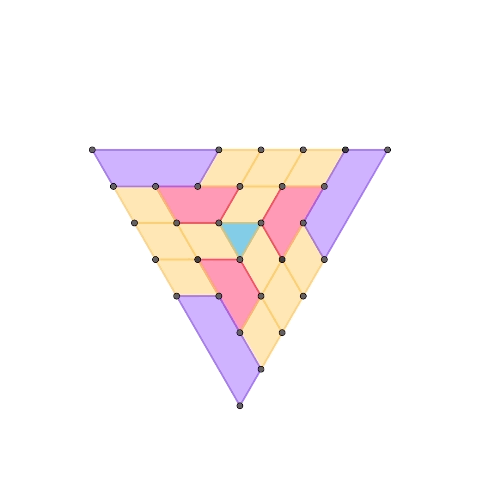
正三角形、正三角形2つで構成されるひし形、正三角形奇数個で構成される台形、によって構成された1自由度機構です。1つ目の機構に更に紫色の台形を要素として加えて拡張したものが2つ目の機構です。台形の種類を増やすことで同様の規則で機構を拡張していくことが可能です。
Honeycomb hinged tessellation with Truchet
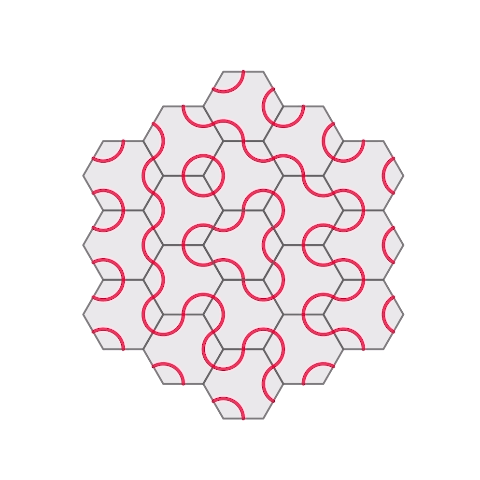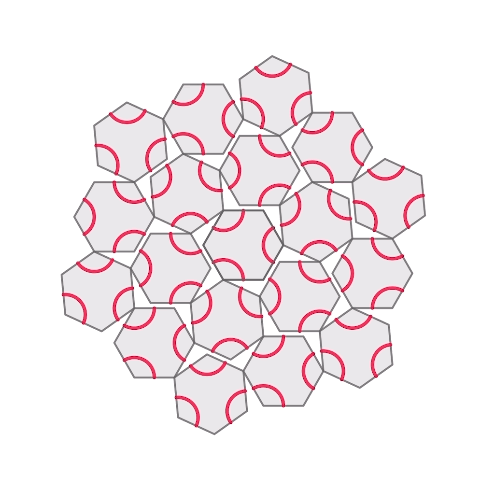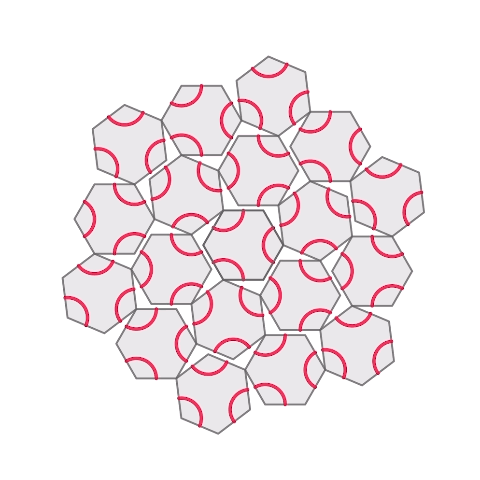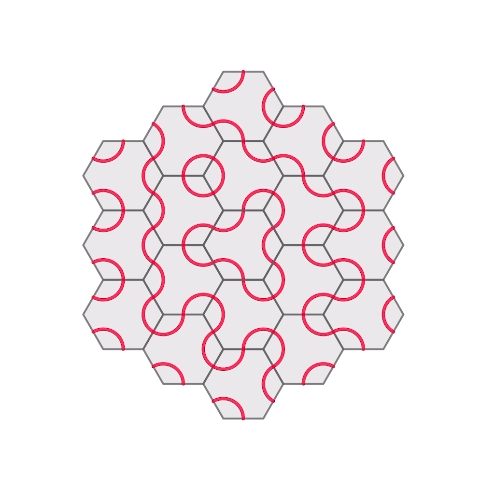
以前作成した正六角形のhinged tessellation上に、truchetの模様を描きました。回転をしても赤い線同士はぴったりとくっつき、違う模様が現れます。


実際に3Dプリントしました。2枚目の2色のものは3Dプリントの途中に一時停止コマンドを設置し、そこでフィラメントの色を入れ替えることで多色での印刷をしています。
正八角形と斜方立方八面体の機構
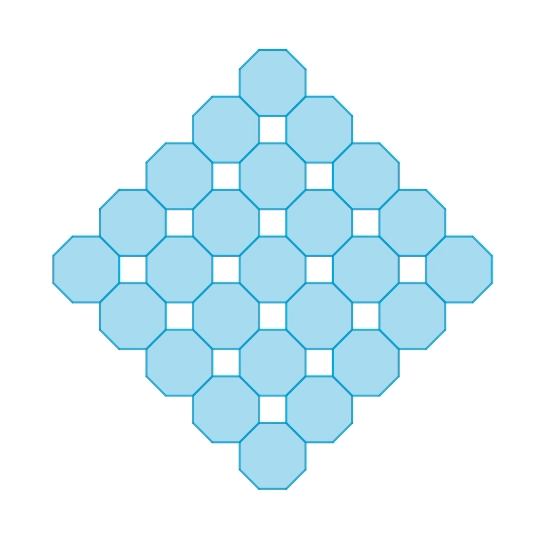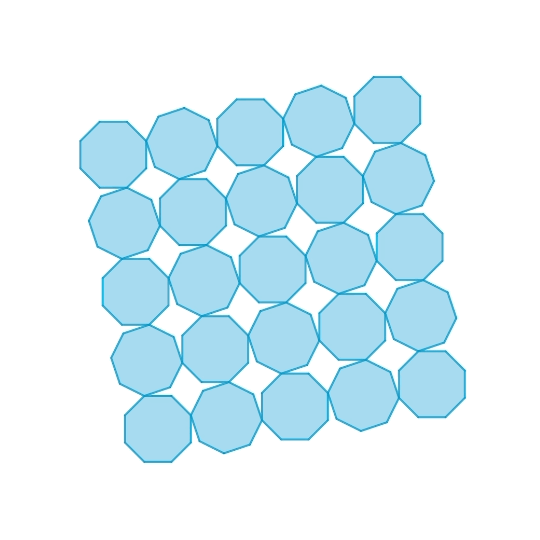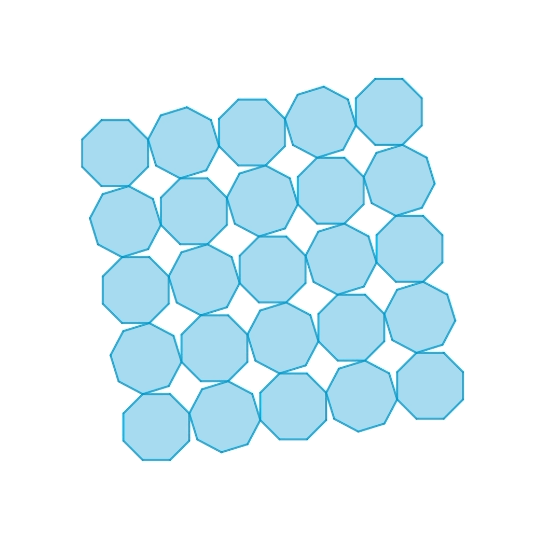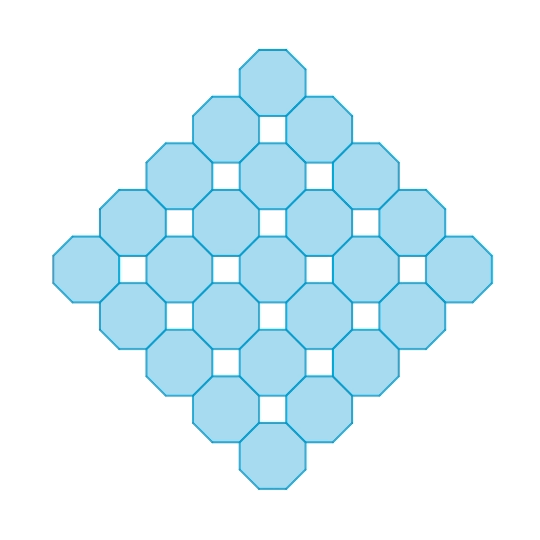
正八角形を繋いだ1自由度機構です。本質的には一般的な正方形のhinged tessellationと同じものです。

先ほどの正八面体を斜方立方八面体に置き換えてみました。

さらに立体的に拡張してみました。この構造はおそらく1自由度ではありません。
Hinged rhombic dodecahedra


先ほどの斜方立方八面体と同様の方法で正方形のhinged tessellationを菱形12面体に拡張しました。
おわり