近況報告
つながるかたち展03に行ってきました
東京大学駒場博物館で開催されていたCONNECTING ARTIFACTS つながるかたち展03を見に行ってきました。展示を主催している舘知宏研究室の研究員である天童智也さんに展示を案内していただき、解説をしていただきながらじっくりと全ての作品を鑑賞しました。幾何学や機構などに興味がある僕にとっては、非常に刺激的で楽しい時間でした。その後は舘研究室に遊びに行かせてもらって、そこの学生の方々とお話をしたり私の作品を少しお見せしたりとこれまたとても楽しかったです。ありがとうございました。
つながるかたち展03はこのブログの執筆時点で展示を終了していますが、同様の展示であるつながるかたち展2.5は2024年1月14日までNTTインターコミュニケーションセンターで開催されていますので、ぜひ足を運んでみてください。
https://www.ntticc.or.jp/ja/exhibitions/2023/connecting-artifacts-2-point-5/
デザインフェスタvol.58にて出展しました

11月11日と12日に東京ビッグサイトで開催されたデザインフェスタvol.58に出展者として参加してきました。たくさんの方にお越しいただきとても楽しい2日間でした。3Dプリントした機構の販売も行い、予想よりも好調な売り上げで在庫の2/3ほどが無くなりました。
私の機構は一見すると変形できるものだと思われないようで「ただの幾何学模様か」という風に興味を失いかけた方が、私のデモンストレーションをみて驚いた様子で二度見して立ち止まってくれるという場面が何度もあって、それが特に僕にとっては楽しかったです。たくさんの方が驚いてくれるのでまるで手品師にでもなった気分でした。
BOOTHでの販売を開始しました
3Dプリントした変形機構の販売をBOOTHで開始しました。まだ1つしか商品がありませんがどんどん増やしていく予定です。よろしくおねがいします。
https://keishiroueki.booth.pm/
海外向けにEtsyなどでショップを開設することも考えています。そちらもこうご期待!
AnkerMake 5MCを購入しました
3台目の3DプリンターとしてAnkerMake 5MCを購入しました。ブラックフライデーのセールで購入して4万8000円ほどでした。流石に今メインで使っているBambu Lab X1-Carbon (オプション込みで25万円)と比べると見劣りする部分は多いですが、5万円以下で購入できるものと考えると非常に優秀でコスパが良いなと感じています。私がよく使っているTPUフィラメントもそれなりにうまく印刷できるので、今後はサブ機として愛用していくつもりです。
11月のまとめ
平面的なhinged tessellationから多面体への拡張
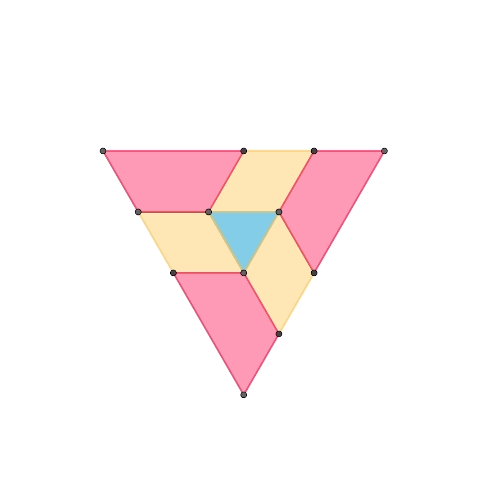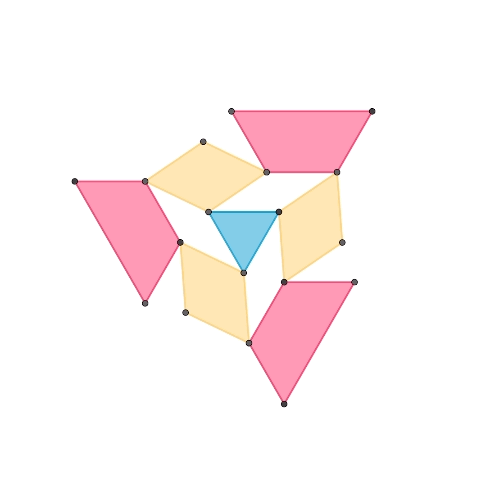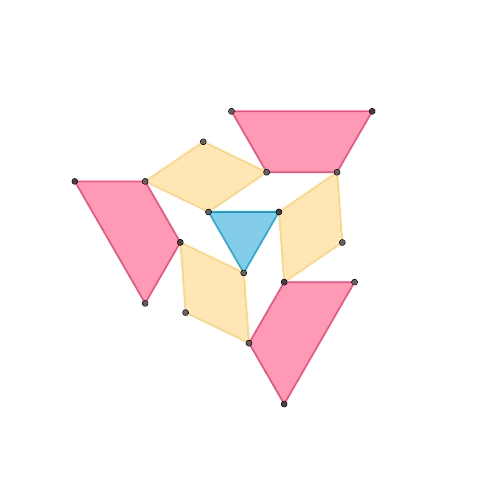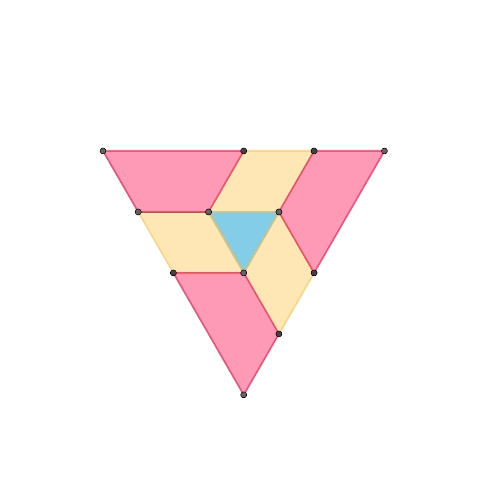
上のアニメーションは10月に作成したものです。外側の台形は中央の正三角形と平行に動作しています。この性質により、この正三角形の平面機構を複製して、それぞれの台形の底辺で接続することで任意のデルタ多面体を構築できると考えました。



その考えのもとに構築した正四面体、デルタ六面体、正二十面体です。辺同士がきっちりと固定されている部分と、辺同士が滑り対偶となっている部分があります。
このアニメーションをXとInstagramに投稿するとそれぞれのプラットフォームから「正八面体であれば滑り対偶なしに機構を構築できるのではないか」という旨の指摘を受けました。指摘をいただいたのはa p uさん (@apu_yokai)と舘知宏さん (@LabOrigami)です。舘さんは先ほどの近況報告で登場した研究室の先生です。お二人ともありがとうございました。
この指摘を元に作成したアニメーションと実際に3Dプリントした模型が以下のものです。


また、正方形の平面機構から立方体を作れないかと考えて試したものが以下のGIFです。

このツイートを受けて、XのフォロワーであるNON_SAKさん (@non_sak)がこのような紙パック工作を作ってくださりました。
立方体の中まで詰まっていて予想外の動きをしていて、とても面白いです。感銘を受けて僕も3Dプリンターで同じ構造を再現しました。

また、Grasshopperでアニメーションも作成しました。まずはそのまま同じものを再現し、そのあとにそれを4つ連結した構造も作ってみました。


また、正方形と正三角形を面として有する多面体の構築についても同様の手法で実現できないかと模索していました。まだそれを実現することはできていませんが、その過程で生まれた正方形の平面機構がこちらです
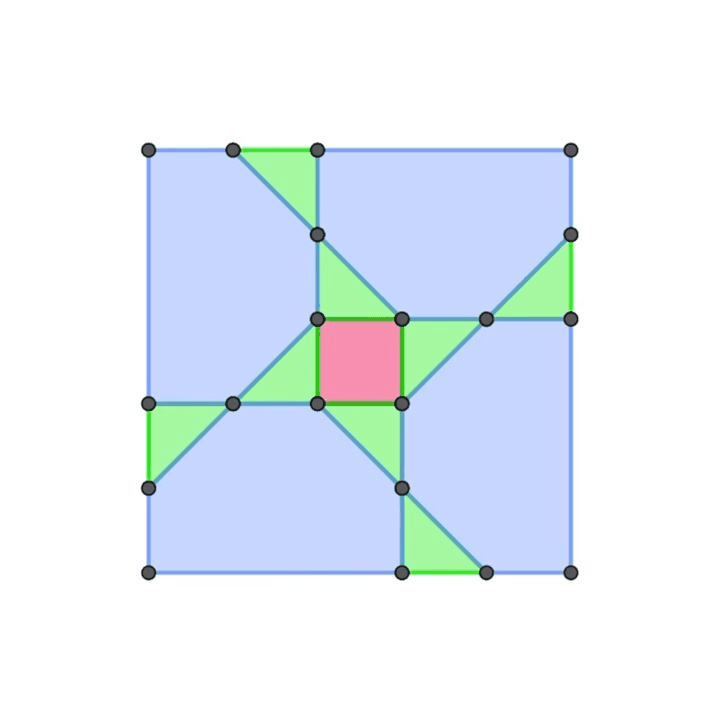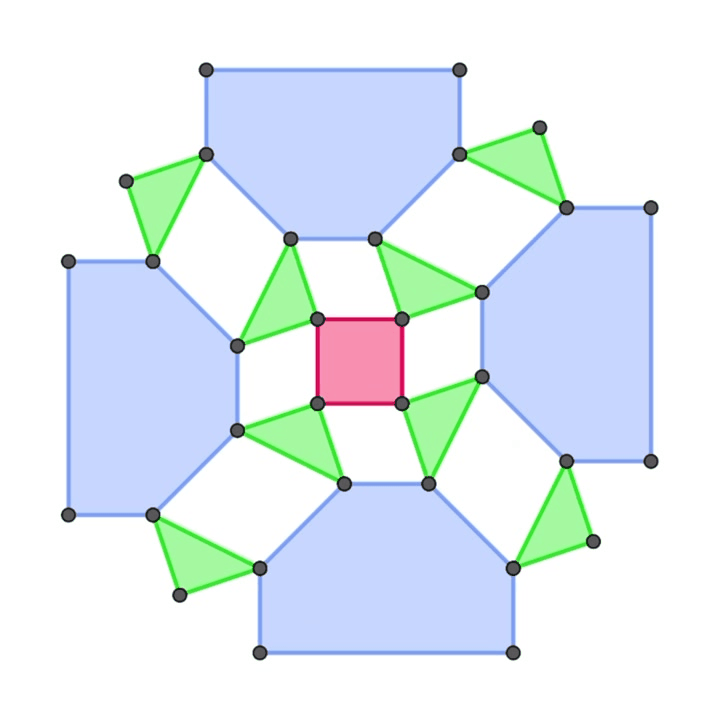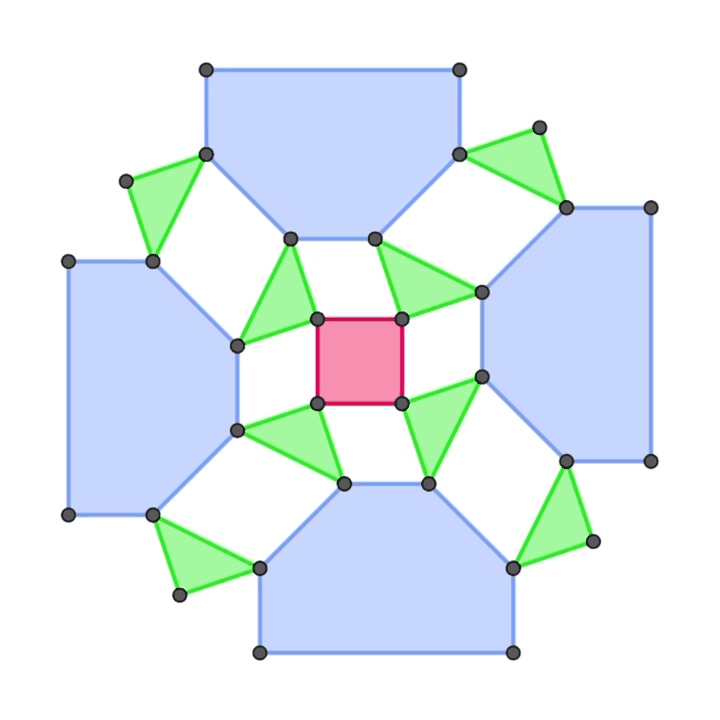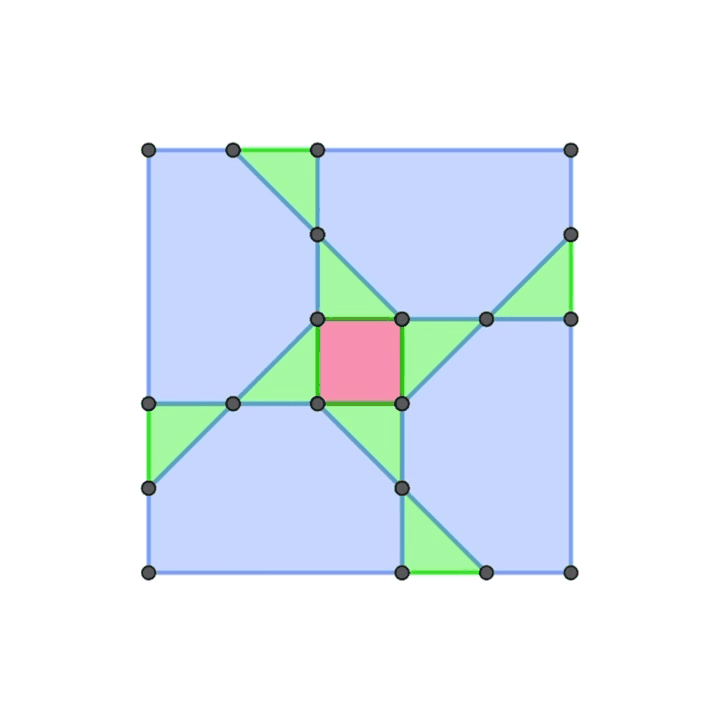

折り紙チューブ
つながるかたち展03で見たおりがみ構造を見よう見まねで3Dプリントしました。
参考:
固くて柔らかいオリガミ展開構造物 https://origami.c.u-tokyo.ac.jp/ZipperTube/

ひょうたんみたいなリンク機構
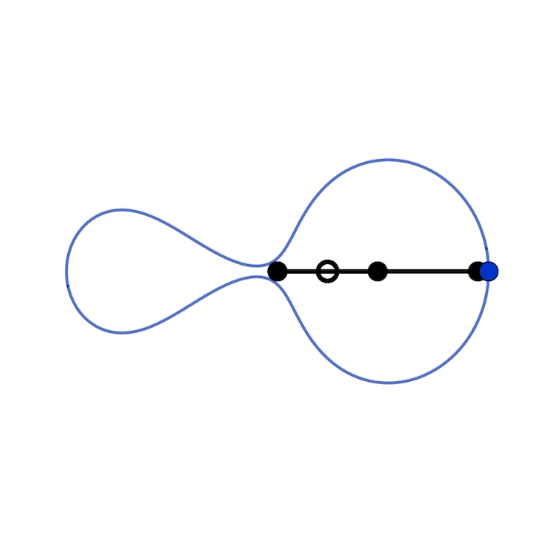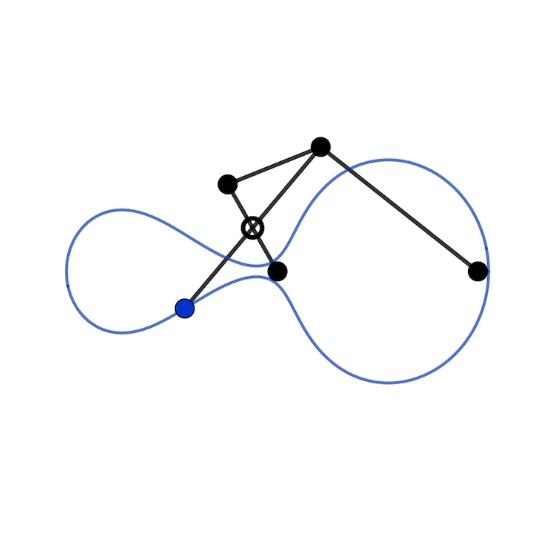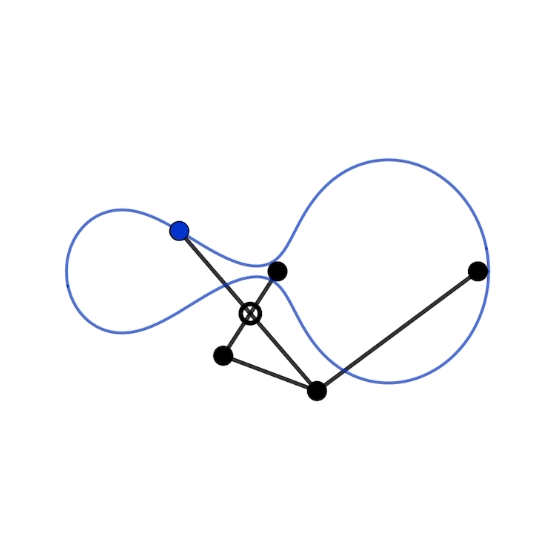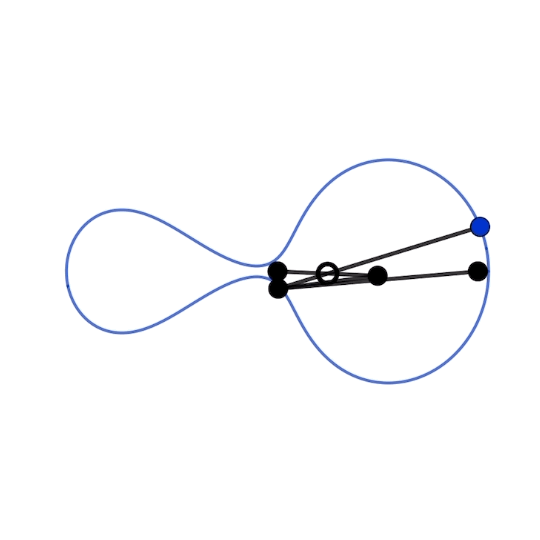
ひょうたんのような軌跡を描く平面リンク機構です。anti-parallelogramとWittgenstein’s rodの組み合わせで構成されています。
リサジュー曲線を描くリンク機構
リサジュー曲線を描くリンク機構です。Kempe’s univesality theoremの簡易版のような手法で構築しています。一応自分で考えついた手法ですが、探せば同じことをしている人はいそうな気がします。
星
星がくるくる回転します。Cults.のクリスマス3Dプリントコンテストのために作りました。

おわり