Update on my current situation
I went to Maker Faire Tokyo 2023
I went to Tokyo on October 15th and attended Maker Faire Tokyo. I saw many wonderful creations and was greatly inspired. I would like to participate as an exhibitor next year.
Preparing for exhibition at Design Festa
I will participate in Design Festa vol. 58, held at Tokyo Big Sight on November 11th and 12th. My booth number is K-178, located on the 4th floor of the West Hall. I will display and sell geometric structures 3D printed with a flexible material (TPU). If you are interested in 3D printing structures with TPU, please also check out 3D print a deforming structure with flexible material. This is my first time selling items at a real event, so I’m unsure how much stock to prepare, how to price items and other details.
Summary of my creation on September
Hinged cubes

This is an animation of the mechanism that was 3D printed in September. The 3D printed version is below.

Origami structure with TPU

Last month, I dropped out of university. And when chatting with an ex-laboratory member on social media, I noticed that her profile image had changed to a GIF animation of an origami structure created with GeoGebra. That animation was interesting, so when I asked her about it, she mentioned that she was inspired by a lampshade she saw in a Japanese food restaurant. At that time, I was contemplating whether I could create origami structures by printing thin TPU, so I asked her to send the GeoGebra ggb file from her, converted it to an STL file for 3D printing, and created it with my home 3D printer. The image below is of the lampshade she photographed in the Japanese restaurant. It appears to be a product from the “IN-EI ISSEY MIYAKE” series.

This structure that transforms by folding doesn’t seem to be a rigid mechanism (I’m not very familiar with origami, but it’s not what’s commonly known as “rigid folding”). For it to fold, deformation is required not just at the creases but in other parts. In the first GIF, I 3D printed with a flexible TPU material. However, when I tried printing with PLA, which is harder than TPU, it didn’t deform properly and cracked at the crease.
Expanding of kite four-bar linkage
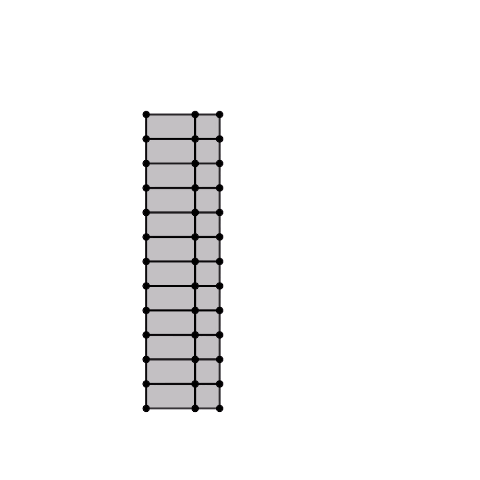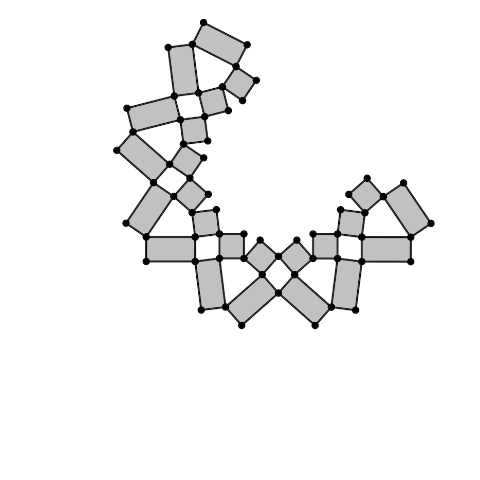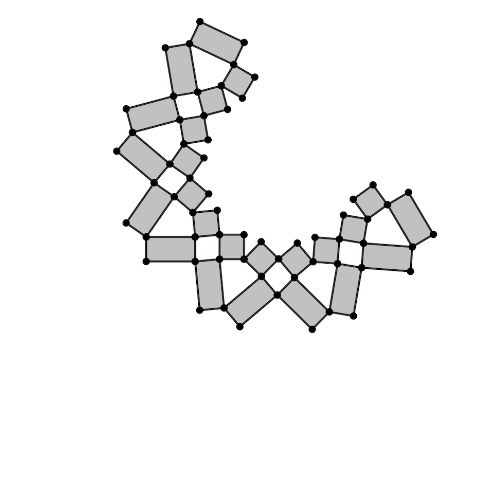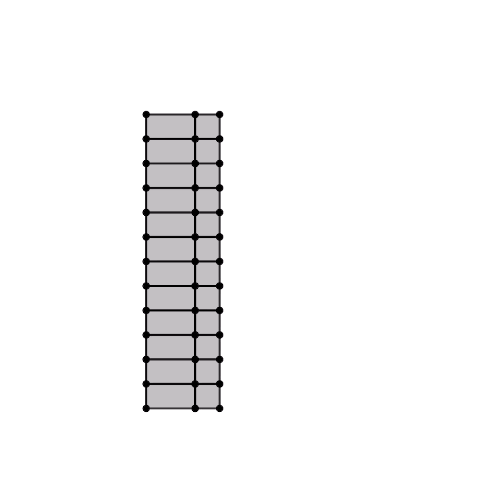
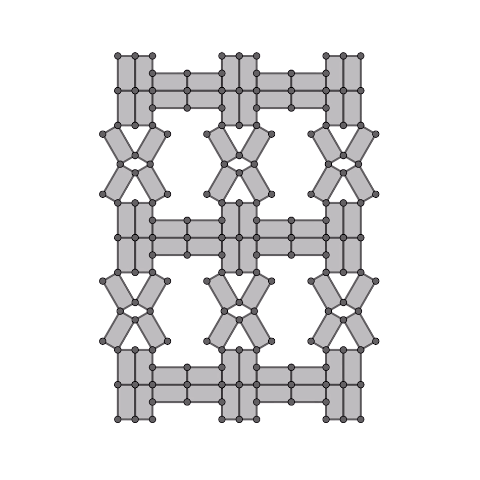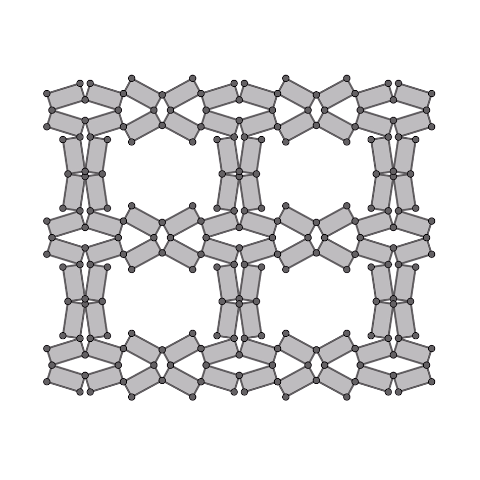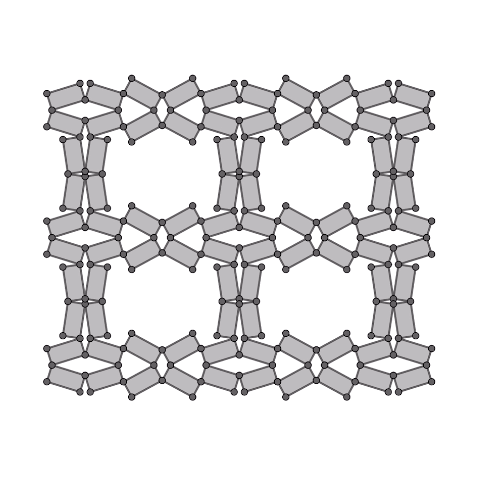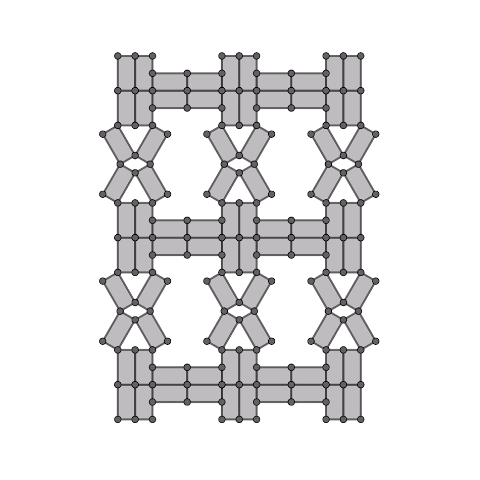
Generate rectangles from the edges of the kite four-bar linkage and connect them.
Hinged tetrahedra

This is a 1-DOF mechanism that multiple tetrahedra are connected by hinges. I believe the original idea was based on a tweet by Daniel Piker (@KangarooPhysics) from a few years ago, but I couldn’t find that post. In the image above, the tetrahedra are 3D printed with PLA and are joined together using tape.


These are whole 3D printed by TPU. And add some tetrahedra.

I tried making it even larger. This wavy movement isn’t originally possible and is allowed due to the softness of the TPU. If I tried to achieve this movement with the PLA and tape combination from the first image, it would probably break immediately.
One of my favorite aspects is how the reflection of light changes as it deforms.
1-DOF planar mechanisms based on regular triangle
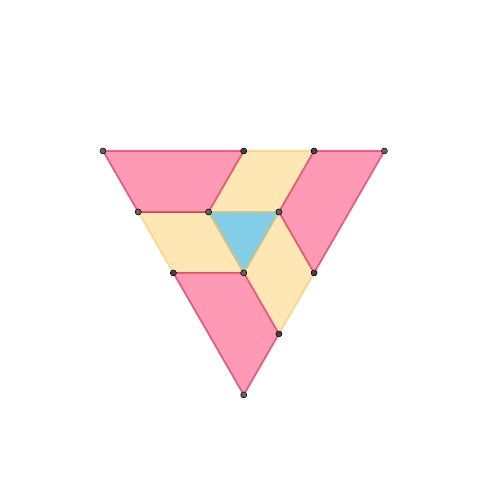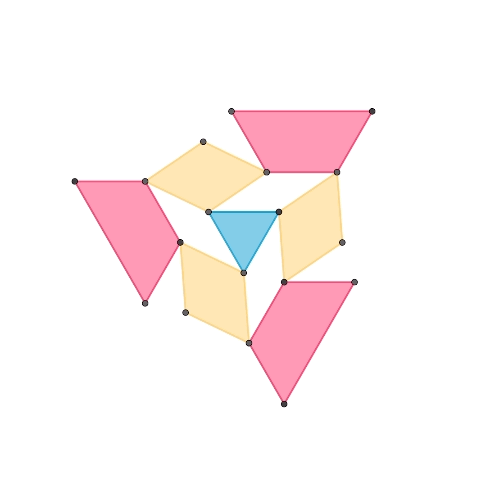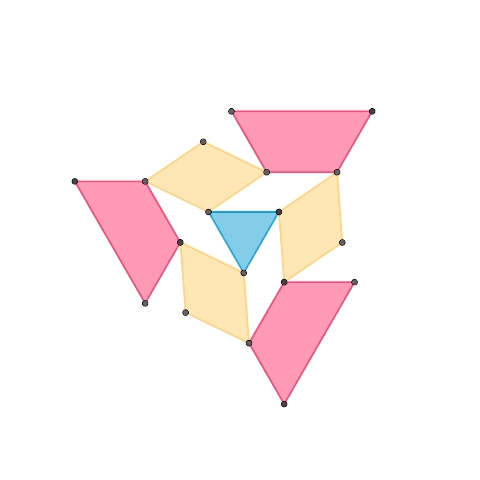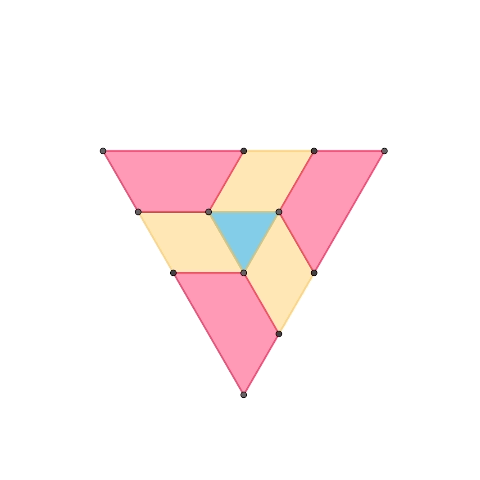
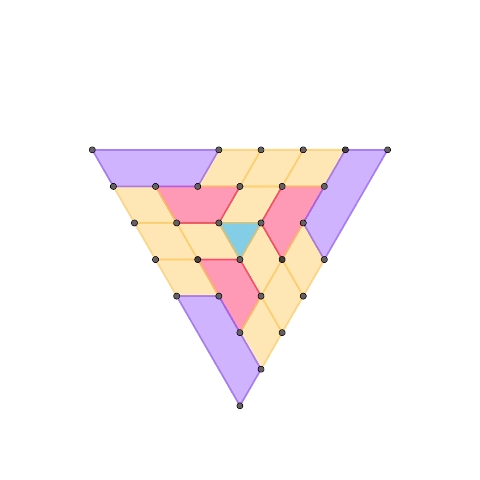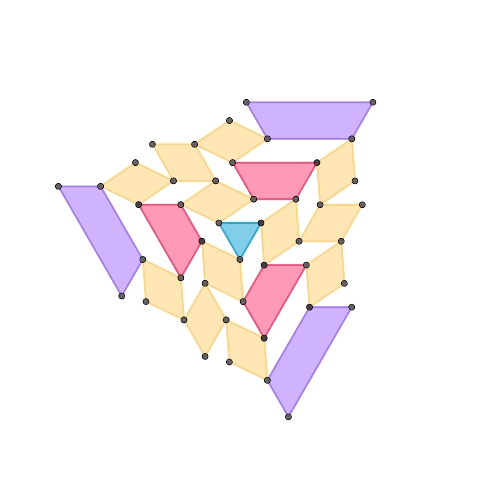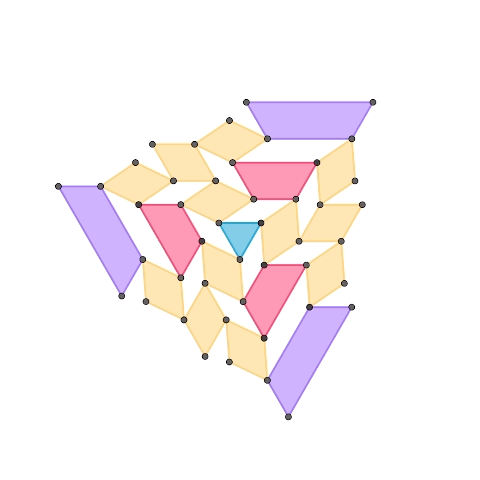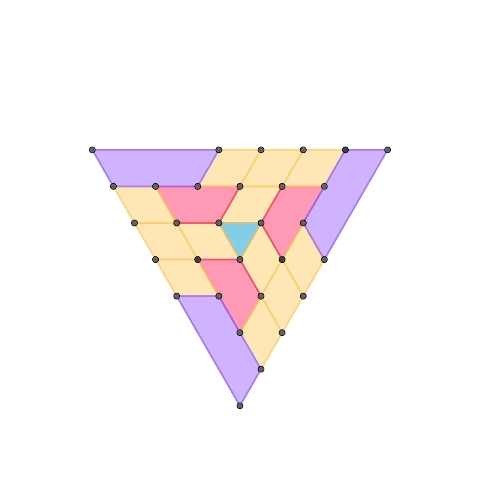
This is a 1-DOF mechanism composed of three elements: a regular triangle, diamonds made of two regular triangles, and trapezoids made of an odd number of regular triangles. The second mechanism extends the first one, adding a purple trapezoid element. By increasing the different shapes of trapezoids, it’s possible to expand the mechanism following a similar pattern.
Honeycomb hinged tessellation with Truchet
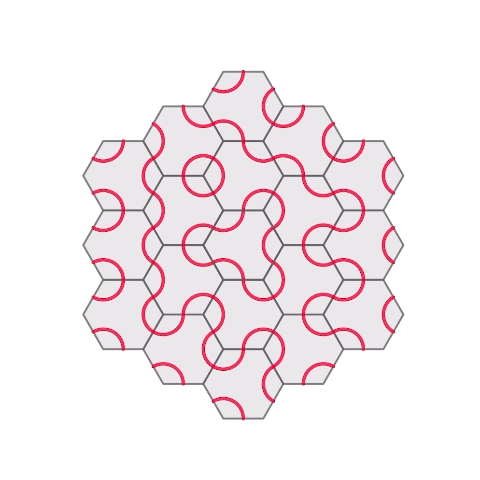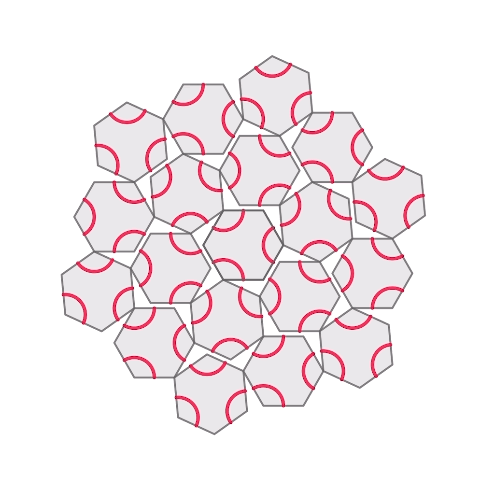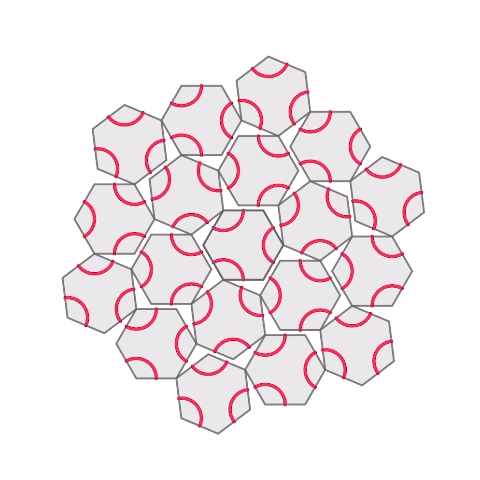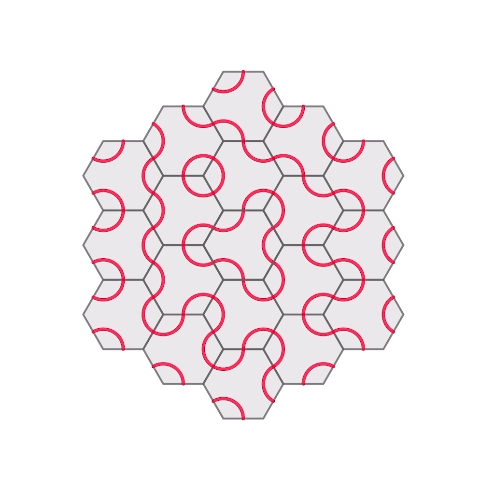
I put a truchet pattern on the hexagonal hinged tessellation I made before.


3D printed. For printing with dual color, I put a pause command between the base part and truchet part.
Mechanisms of regular octagon and rhombicuboctahedron
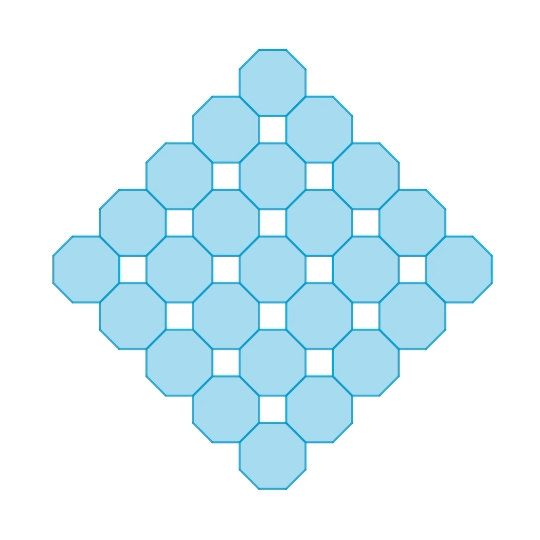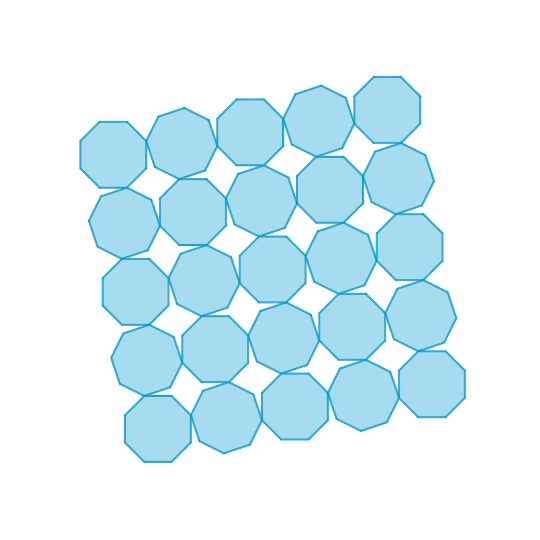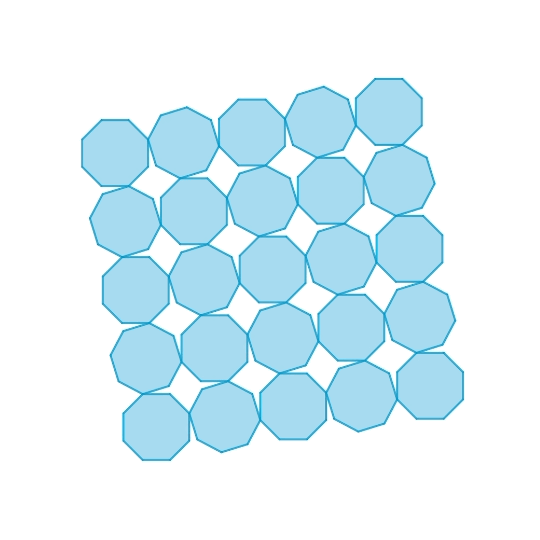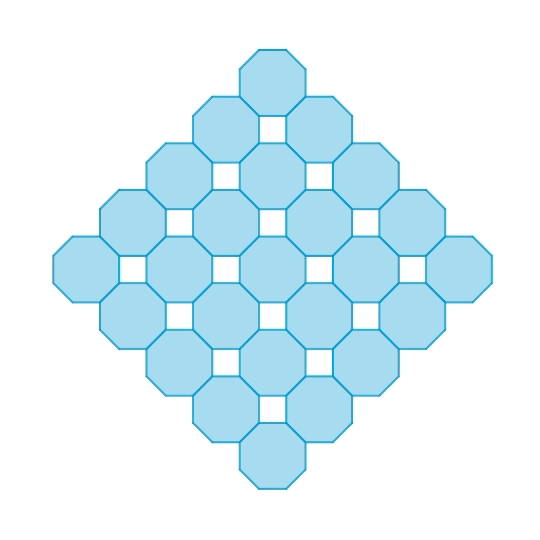
This is a 1-DOF planar mechanism composed of regular octagons. Essentially, this is the same as a typical square hinged tessellation.

Replaced regular octagon into rhombicuboctahedron.

I expand more spatially. This mechanism might not have 1-DOF.
Hinged rhombic dodecahedra


Using a method similar to the earlier rhombic dodecahedron, I expanded the square hinged tessellation to a rhombic dodecahedron.
Thank you for reading!